Note: this is a deviation from the applied projects I usually present, and is not to be taken too seriously. There may be mistakes in the math somewhere (and if you can point them out, please let me know), but I still liked the idea as a blog post. In fact, this is probably my favorite post yet.
Also, sorry about the varying sizes of the expressions. I know it looks ugly, but I did my best.
Also, sorry about the varying sizes of the expressions. I know it looks ugly, but I did my best.
Theory
Let’s imagine that an
individual’s, i, self-satisfaction, SS,
can be defined as a multivariate linear model, such that:
Where P is defined as controllable factors pertaining to one’s profession, R as controllable factors affecting one’s relationships and c as a vector of other controllable factors that affect one’s self-satisfaction such as hobbies, religiosity, etc (its coefficient also a vector of betas). Then, u represents all uncontrollable factors that affect one’s happiness—things pertaining to luck: whether one wins the lottery, etc.
For obvious reasons,
any such model would be impractical in the real-world if
1.
P, R, and
c were exogenously fixed by someone other than the individual
2.
The model did not vary over time
Therefore, we can rewrite the
model as:
Where
t is meant to denote a discrete
period of time, and (.)
If
we can accept this, then we can further decide that the variables of the multivariate model (except u) are not just controllable, but fixable by the individual. If that is
the case, then the model can further be rewritten as:
Where
k is now some fixable element function factored out of the equation. Alpha terms
are now:
The
term ut is therefore unaffected.
The importance of writing the function this way is that we can now plot self-satisfaction
in a temporal space. We can also determine a theory of how one would best fix k so as to maximize one’s
self-satisfaction.
But
before doing this, we need to make one more assumption, the biggest assumption
of the theory, and that is:
Where Ε is an expected value operator and t0 is any discrete unit of
time (it can be right now, for example) less than T. T can reasonably be defined as the amount of time the individual
will live, probably given that he/she doesn’t die an early, unfortunate death. In
layman’s terms, over the course of one’s life, and starting anywhere in
it, one will be as unlucky as lucky. The uncontrollable bad parts of life will
be negated by the uncontrollable good things, assuming the uncontrollable bad things do not include one's own death.
We can then conclude:
Meaning the sum of
one’s lifetime self-satisfaction is the sum of the controllable parts of one’s
life described in a multi-linear model. I imagine this framework might be controversial to some, and if so, it is probably because of the assumption
made in regards to ut.
Some people’s lives are simply unlucky on the aggregate. Other people’s are
disproportionately lucky. I acknowledge this fact and admit it can be a
weakness to the theoretical framework. But if we can agree that the assumption
made in regards to ut is
even approximately correct for most
individuals, or that
then I think we can continue down this path.
The most important question then, is how do we fix k such that SS is maximized in any given time, t, expressed as:
The most important question then, is how do we fix k such that SS is maximized in any given time, t, expressed as:
And I think the
naïve answer would be to say that
Such that one’s
self-satisfaction continually increases as time passes at a constant rate, with
some (positive) intercept unique to the individual, ii. If one assumes they know the units of SS, then they
should add a slope coefficient, ø to
the model. In my mind, the model would best be written with units of SS such
that 0 < ø < 1 so
that one’s self-satisfaction only increases in proportion with t less than t itself, but still positively. Writing the function this way, ø describes a reasonable pace in which we can continually increase
our SS over time that can easily be compared to time and that can also easily be plotted. And one could theoretically even write ø as
a function such that:
But, to simplify
things, I am content on holding ø constant:
But,
I think saying that self-satisfaction will always increase linearly with t is somewhat naïve. Do we know anyone
who actually functions this way? I don’t. And I don’t think it’s realistic nor possible. I
would propose something like this:
Or,
that self-satisfaction approximates a wave function that increases over time. Note:
the sub-notation i for individual has
been dropped for now. Some people are born naturally more satisfied with life than
others, denoted by ø0, and t0 is
added to clarify that whenever one decides to start fixing k in this way, SS can be maximized over the interval {t0, T}.
On
a plot, it looks like this:
Where
self-satisfaction ebbs and flows but generally increases.
If
this is a valid way to define optimal self-satisfaction over time, then I can
see joy (j) being defined as a differentiation of this function with respect to
t such that:
In
other words, anywhere on the above plot where the slope of the function is
positive (self-satisfaction is increasing), joy is experienced by the
individual, but anywhere where it is decreasing, joy is negatively experienced,
and we can call this distress. This seems right, but if this is the case, then
a curious phenomenon is exposed:
During
the interval of time given in example A, the individual is experiencing joy and
in example B, distress. This is curious because
in the interval given in example B, the individual has also obtained more
self-satisfaction than he/she had in example A, and yet, is not experiencing joy.
This seems paradoxical, but really maps onto our real-world experiences.
There are times where we know we have a lot, have come further than we were
before, but somehow are just not as happy in the moment. If self-satisfaction
is a wave function as described above and joy is a first partial derivative
with respect to time, then why this is is successfully modeled.
There
is one more element here worth introducing, and that is the idea of self-worth (SW). In
political terms, we think of the self-worth of any individual as some
arbitrarily high constant (a) such
that:
This
has important political implications. It is smart to begin our baseline
assumption about politics as if everyone were worth the same, everyone were
worth a lot, that everybody’s worth did not change over time, etc. If this is
the model we operate with, then we will be better off as a society with more
equitable treatment of everyone.
However,
in reality, this is not how self-worth works. We become more or less valuable to
our jobs over time, our role in our relationships become stronger (or weaker) and there
seems to be some overall variation. If the variation is related to
self-satisfaction, I can see self-worth as a linear approximation of
self-satisfaction over time such that:
And
I suppose this would become a piecewise function over intervals of different
fixed k. If we are living our life
with an optimal wave-function of self-satisfaction, as defined already,
then this linear approximation can be described as:
or, something that equals our naïve definition of self-satisfaction (given that t0 + ø0 = ii). I additionally argue that no error term is needed here as it is impractical to think of self-worth being reliant at all on luck—this causes SW to be biased in some periods—if we hold that it is really a linear approximation of SS—but the bias is negated over time as long as the assumption related to ut holds. In summary, we should generally become more content over time, and we don’t. But this “should” pervades. This “should” merely describes our self-worth function, not overall self-satisfaction. This can be plotted:
And
what this means practically is that although our self-satisfaction ebbs and
flows (but generally increases) and our joy can be on or off at any given time,
our self-worth remains growing at a constant rate. We’re never as good as we think we are when we think we’re good, and we’re never as bad as we think we are when we think we’re bad. Our self-worth is time stationary, growing
the same as we work for optimally increasing self-satisfaction.
It
makes me think of the John Wooden quote:
“You
can't let praise or criticism get to you. It's a weakness to get caught up in
either one.”
Except, I wouldn't say it's a weakness. It’s just math.
So,
how do we ascertain the optimal amount of self-satisfaction? It boils
down to intentionally weakening our professional lives, relationships and
other controllable factors so that they can eventually become stronger over time.
Like lifting weights. It’s this process of destroying each piece of our lives intentionally and deliberately and then letting it re-form into something better as time passes. That’s how
we should fix k to optimize SS, and if we do that,
our lives become maximally satisfying over time and throughout every controllable dimension that determines our self-satisfaction. Knowing this is practically useful; if we’re not as happy now as we want to be, the mathematical framework suggests we’ll bounce back later, leaving our moments of distress less impactful.
Of
course, we used mathematical tricks to be able to ignore ut —the uncontrollable factors that influence our self-satisfaction. Because of its presence in any given period, we cannot ever live in
exactly this way. Luck often plays a role to make us disproportionately
happy/sad in a given period. But we can control what we can control. And when
bad luck occurs this period, we wait for life to even out, remembering self-worth is not reliant on luck. Never too up nor too down. Just focused on our goals and being sure about the ways we go about
achieving them. And that's all there is to it.



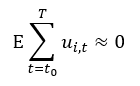

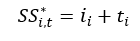

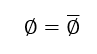









No comments:
Post a Comment