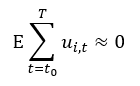Gun Laws, Gun Violence, and Washington DC

By Michael Keith & Grace Allen

Introduction

Kaggle maintains a dataset documenting over 225,000 incidents involving gun crime from January 2014 through December 2017 across the United States. This dataset includes the number of people injured and killed as well as the date and location of each incident. I combined this dataset with a dataset I already had on hand, the NICS data maintained by the FBI on the number of background checks submitted by firearms vendors, which I have worked with previously. My friend from grad school, Grace Allen, also helped me locate and analyze data on the number of gun laws as well as the number of outstanding residential firearms licenses in each state. Our goal was to determine whether any of these factors could be shown empirically to drive casualties related to gun violence.

Statewide gun laws reveal how legislation directly affects gun violence across states. The number of outstanding firearms licenses may serve as a proxy revealing attitudes toward guns—the more licenses outstanding (per resident in the state), the more positive the citizenry feels about guns generally. If these data can successfully be used to model and predict gun violence, a level of nuance is added to some of the analyses I've performed previously with the result of deriving more interesting conclusions.

When it came down to running some statistical models, it was difficult to draw statistically significant relationships. We tried slicing the data many ways—modeling across states per month, across months per state, etc. But ultimately, we think the problem is a lack in the quantity of data to make strong conclusions. Four years of data can’t be expected to reveal long-term trends in most cases.

In addition to the non-statistically significant results, there were some more decisive findings, but the conclusions we could draw from them weren’t that interesting. For instance, we were able to conclude with a strong degree of confidence that gun violence is influenced in a positive direction by the unemployment rate in a state at any given time. But the relationship is small and most people probably could have guessed that some kind of such correlation existed. What we really wanted were answers to bigger questions: how do gun sales affect gun violence? Are laws effective in reducing gun violence? Does the general statewide attitude toward firearms make a difference?

It could be that strong relationships just don’t exist in this space. There may just be no causal link to find. But, we are open to all ideas and will try anything that’s worth exploring. If you are interested in seeing some of the results of the models we ran, want to suggest other ways to use the data, or have ideas about different data sources that can be used, please let us know by leaving comments.

Note: We don't believe the data we have on gun-related casualties is representative of every incident over the time span. For instance, there is no inclusion of accidental or self-inflicted gun violence. However, where data is missing, we assume it is randomly dispersed across all states in any given time period. This means a valid, statewide analysis can be performed.

Correlations

There were some relationships relationships that could be explored as well as some correlations anyone would be interested in seeing. We feel it’s necessary to state that the following results are not indicative of any kind of causation. We simply go through a series of questions and attempt to answer them with the best guesses the data can provide. For a complete look at the dataset we used to compile these graphics, see here.

How do gun laws affect gun violence? To answer this question, we used data maintained by the Rand Corporation to track how many restrictive (or non-permissive) gun laws existed in each state in the time span we had available to us. As one might guess, there was not a lot of variation from the first date to the last across states—states don’t pass new restrictive laws very often. But, taking the average gun laws per state over the 4 years as well as the average gun-violence rate (defined as the number of casualties afflicted by gun-crime related incidents per 10,000 citizens) in each state, we constructed the following plot:

We do see a slight negative correlation—states with more restrictive gun laws see less gun violence generally. But again, there is a lot of variance in this relationship and the effect is small. The relationship we do see can possibly be explained by other factors.

How do residential licenses affect gun violence? Residential licenses outstanding per citizen in the state can be looked at as a proxy for attitudes toward guns—under this theory, the more licenses outstanding, the more positive that state feels about guns. Do states which think more positively about guns see fewer casualties? The answer is a strong “we don’t know.” There may be a slightly negative correlation, but this was one of the least interesting relationships we explored because the data seemed so randomly dispersed.

So, there it is. Make of it what you will.

How do the number of background checks submitted to the FBI affect gun violence? The number of background checks submitted for long gun and handgun purchases per 10,000 citizens was plotted against the gun-violence rate and a positive relationship was extracted. Out of all the relationships we explored, by simply eyeballing the data, this seemed to be the strongest:

This data can be used as a proxy for gun sales—previous research suggests that the number of background checks submitted to the FBI are highly correlated with the number of gun sales. But again, we can’t make any strong conclusions about causal relationships based on the plot drawn above.

How does Washington DC factor into all this? Washington DC appears to be an outlier in every way. Its gun-violence rate is extremely high when compared to the states, but there are not a lot of background checks being submitted to the FBI from there. When it is added to the last graph displayed above, it looks like this:

By itself, it completely reverses the sign of what appeared previously to be a somewhat strong relationship.

It’s likely that a large part of this result has to do with the way the data is sorted. Washington DC has many qualities that are more characteristic of a large city than a state. To start, a huge share of people who work in DC are actually residents of surrounding states such as Maryland and Virginia. So, any licenses or firearms registered to these commuters would be counted under their home state, while any crimes they commit in the city would be counted under Washington DC. Also, because the population of DC has been reported to increase by as much as 72% during the daytime, the typical method used to calculate per capita statistics may not fit here. For example, if there are one million people in the city during the day, and 10 crimes occur, then there was 1 crime for every 100,000 people present. But if the number of crimes per capita is calculated using the number of residents (about 600,000), then this statistic could be reported at 1.6 crimes for every 100,000 people, nearly double. This effect could also be present in other large, commuter cities like New York or Atlanta, but in those cases, the commuters are likely commuting within their home state. Because DC does not belong to a state, it may be forced to claim casualties that are actually more directly related to the regulations and culture of the surrounding states than its own. It’s important to remember that these are only hypotheses, not conclusions, and further research would be needed to test these ideas.

Aside from data collection quirks, there are other attributes of DC that could make it very interesting to study in terms of this issue. Some possible reasons for the strange results may be due to DC’s status as our nation’s capital. Washington DC is home to many prominent political figures and government agencies, which requires that the district provide a greater level of security than the average city. Residents of the District of Columbia must be licensed and wait 10 days after purchasing a firearm to take possession of it, and every firearm owned by a resident must be individually registered with Metro PD. While the actual laws regarding the possession of firearms in DC are on par with many other states, some of them are much more relevant there than in other places. For example, it is illegal in all states to carry a firearm on federal property. In most cities, this would mainly apply to the post office and the court house, but in DC this applies to a much larger share of the city’s buildings and land area. So, in practice, DC could be said to have greater restrictions than most US states. DC also imposes a 10-round limit on magazine capacity and a ban on assault rifles. The fact that DC enforces many hotly debated gun control laws, and produced such strong and unexpected results, suggests that it may be worth it to investigate ways to more accurately measure the effects of gun legislation in this area.

Conclusion

As far as we are aware, no study proving a causal link between any of the variables we explored has been accomplished. At best, there have been hypotheses made using good arguments and sound methods, but nothing that is ultimately conclusive. Therefore, there is still an open debate about the exact nature of the relationship between all these factors. Although we can view certain correlations, more information, more data, or better ways of modeling the data is needed before strong conclusions can be drawn.

We also discussed Washington DC and why it may be a case worthy of consideration by itself. It certainly appeared to be an outlier in these categories by a pure numbers’ standpoint. And we think it’s important to keep that in mind. A lot of people use Washington DC as an example of why there definitely is no relationship between gun sales, gun laws, and gun violence, or that the relationship we think exists really doesn’t, but that’s like using an exception to prove the rule. Better ways of thinking about DC is needed before it is used as an example in this domain.

In summary, we can make good guesses and create informed hypotheses about how the relationships explored should look, but the right data to know for sure one way or another is just not available. If you disagree or have any other comments, feel free to let us know.

DC - Citations

If you want to research more about Washington DC, here are the resources we used:

• General DC gun laws - https://www.pewpewtactical.com/gun-laws-state/washington-dc-gun-laws/
• Where you cannot carry in DC - https://www.pewpewtactical.com/concealed-carry-laws/washington-dc-concealed-carry-laws/
• DC daytime population - https://ggwash.org/view/34772/dcs-daytime-population-is-over-a-million
• DC daytime population - https://www.thoughtco.com/cities-see-huge-daily-population-swings-3320981
• Federal land - https://www.washingtonpost.com/graphics/local/dc-marijuana-map/

Mathematical Theory of Happiness

Note: this is a deviation from the applied projects I usually present, and is not to be taken too seriously. There may be mistakes in the math somewhere (and if you can point them out, please let me know), but I still liked the idea as a blog post. In fact, this is probably my favorite post yet.

Also, sorry about the varying sizes of the expressions. I know it looks ugly, but I did my best.

Theory

Let’s imagine that an individual’s, i, self-satisfaction, SS, can be defined as a multivariate linear model, such that: 

Where P is defined as controllable factors pertaining to one’s profession, R as controllable factors affecting one’s relationships and c as a vector of other controllable factors that affect one’s self-satisfaction such as hobbies, religiosity, etc (its coefficient also a vector of betas). Then, u represents all uncontrollable factors that affect one’s happiness—things pertaining to luck: whether one wins the lottery, etc.

For obvious reasons, any such model would be impractical in the real-world if

1.       P, R, and c were exogenously fixed by someone other than the individual

2.       The model did not vary over time

Therefore, we can rewrite the model as:

Where t is meant to denote a discrete period of time, and (.) represents any arbitrary number of variables that affect the functions of P, R, and c respectively. The term u does not become a function because luck is stochastic and strictly exogenous in this model. The adage if you work hard you can create your own luck does not apply under this framework.

If we can accept this, then we can further decide that the variables of the multivariate model (except u) are not just controllable, but fixable by the individual. If that is the case, then the model can further be rewritten as:

Where k is now some fixable element function factored out of the equation. Alpha terms are now:

The term u_t is therefore unaffected. The importance of writing the function this way is that we can now plot self-satisfaction in a temporal space. We can also determine a theory of how one would best fix k so as to maximize one’s self-satisfaction.

But before doing this, we need to make one more assumption, the biggest assumption of the theory, and that is:

Where Ε is an expected value operator and t₀ is any discrete unit of time (it can be right now, for example) less than T. T can reasonably be defined as the amount of time the individual will live, probably given that he/she doesn’t die an early, unfortunate death. In layman’s terms, over the course of one’s life, and starting anywhere in it, one will be as unlucky as lucky. The uncontrollable bad parts of life will be negated by the uncontrollable good things, assuming the uncontrollable bad things do not include one's own death.

We can then conclude: 

Meaning the sum of one’s lifetime self-satisfaction is the sum of the controllable parts of one’s life described in a multi-linear model. I imagine this framework might be controversial to some, and if so, it is probably because of the assumption made in regards to u_t. Some people’s lives are simply unlucky on the aggregate. Other people’s are disproportionately lucky. I acknowledge this fact and admit it can be a weakness to the theoretical framework. But if we can agree that the assumption made in regards to u_t is even approximately correct for most individuals, or that

 then I think we can continue down this path.

The most important question then, is how do we fix k such that SS is maximized in any given time, t, expressed as: 

And I think the naïve answer would be to say that

Such that one’s self-satisfaction continually increases as time passes at a constant rate, with some (positive) intercept unique to the individual, i_i. If one assumes they know the units of SS, then they should add a slope coefficient, ø to the model. In my mind, the model would best be written with units of SS such that 0 < ø < 1 so that one’s self-satisfaction only increases in proportion with t less than t itself, but still positively. Writing the function this way, ø describes a reasonable pace in which we can continually increase our SS over time that can easily be compared to time and that can also easily be plotted. And one could theoretically even write ø as a function such that: 

But, to simplify things, I am content on holding ø constant:

But, I think saying that self-satisfaction will always increase linearly with t is somewhat naïve. Do we know anyone who actually functions this way? I don’t. And I don’t think it’s realistic nor possible. I would propose something like this:

Or, that self-satisfaction approximates a wave function that increases over time. Note: the sub-notation i for individual has been dropped for now. Some people are born naturally more satisfied with life than others, denoted by ø₀, and t₀ is added to clarify that whenever one decides to start fixing k in this way, SS can be maximized over the interval {t₀, T}.

On a plot, it looks like this: 

Where self-satisfaction ebbs and flows but generally increases.

If this is a valid way to define optimal self-satisfaction over time, then I can see joy (j) being defined as a differentiation of this function with respect to t such that:

In other words, anywhere on the above plot where the slope of the function is positive (self-satisfaction is increasing), joy is experienced by the individual, but anywhere where it is decreasing, joy is negatively experienced, and we can call this distress. This seems right, but if this is the case, then a curious phenomenon is exposed: 

During the interval of time given in example A, the individual is experiencing joy and in example B, distress. This is curious because in the interval given in example B, the individual has also obtained more self-satisfaction than he/she had in example A, and yet, is not experiencing joy. This seems paradoxical, but really maps onto our real-world experiences. There are times where we know we have a lot, have come further than we were before, but somehow are just not as happy in the moment. If self-satisfaction is a wave function as described above and joy is a first partial derivative with respect to time, then why this is is successfully modeled.

There is one more element here worth introducing, and that is the idea of self-worth (SW). In political terms, we think of the self-worth of any individual as some arbitrarily high constant (a) such that:

This has important political implications. It is smart to begin our baseline assumption about politics as if everyone were worth the same, everyone were worth a lot, that everybody’s worth did not change over time, etc. If this is the model we operate with, then we will be better off as a society with more equitable treatment of everyone.

However, in reality, this is not how self-worth works. We become more or less valuable to our jobs over time, our role in our relationships become stronger (or weaker) and there seems to be some overall variation. If the variation is related to self-satisfaction, I can see self-worth as a linear approximation of self-satisfaction over time such that:

And I suppose this would become a piecewise function over intervals of different fixed k. If we are living our life with an optimal wave-function of self-satisfaction, as defined already, then this linear approximation can be described as: 

 Curiously enough, this simplifies to: 

or, something that equals our naïve definition of self-satisfaction (given that t_{0 +} ø_{0 =}  i_i). I additionally argue that no error term is needed here as it is impractical to think of self-worth being reliant at all on luck—this causes SW to be biased in some periods—if we hold that it is really a linear approximation of SS—but the bias is negated over time as long as the assumption related to u_t holds. In summary, we should generally become more content over time, and we don’t. But this “should” pervades. This “should” merely describes our self-worth function, not overall self-satisfaction. This can be plotted:

And what this means practically is that although our self-satisfaction ebbs and flows (but generally increases) and our joy can be on or off at any given time, our self-worth remains growing at a constant rate. We’re never as good as we think we are when we think we’re good, and we’re never as bad as we think we are when we think we’re bad. Our self-worth is time stationary, growing the same as we work for optimally increasing self-satisfaction. 

It makes me think of the John Wooden quote:

“You can't let praise or criticism get to you. It's a weakness to get caught up in either one.”

Except, I wouldn't say it's a weakness. It’s just math.

Conclusion

So, how do we ascertain the optimal amount of self-satisfaction? It boils down to intentionally weakening our professional lives, relationships and other controllable factors so that they can eventually become stronger over time. Like lifting weights. It’s this process of destroying each piece of our lives intentionally and deliberately and then letting it re-form into something better as time passes. That’s how we should fix k to optimize SS, and if we do that, our lives become maximally satisfying over time and throughout every controllable dimension that determines our self-satisfaction. Knowing this is practically useful; if we’re not as happy now as we want to be, the mathematical framework suggests we’ll bounce back later, leaving our moments of distress less impactful.

Of course, we used mathematical tricks to be able to ignore u_t —the uncontrollable factors that influence our self-satisfaction. Because of its presence in any given period, we cannot ever live in exactly this way. Luck often plays a role to make us disproportionately happy/sad in a given period. But we can control what we can control. And when bad luck occurs this period, we wait for life to even out, remembering self-worth is not reliant on luck. Never too up nor too down. Just focused on our goals and being sure about the ways we go about achieving them. And that's all there is to it.